决策树.md

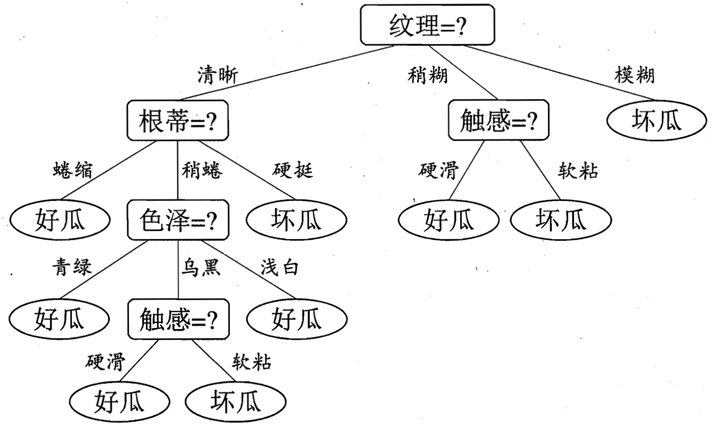
决策树是一个基础的模型，也是许多集成算法的基学习器。决策树即可以解决分类问题，也可以解决回归问题。决策树是树状结构，每个非叶子节点表示一个特征或属性，其分叉表示在该属性上的划分，每个叶子节点表示一个分类。从根节点到叶子节点的路径对应了一个决策序列，下图是周志华“西瓜书”的决策树例子。

决策树的生成：不断递归找到最优划分属性和划分点，直到：

1. 当前节点的样本全属于同一类别
2. 当前节点的样本所有属性值都相同
3. 当前节点样本集为空

生成决策树的核心是找到最优划分属性及其划分点，有多种方法。其中ID3、C4.5算法生成的是多叉树（如果有离散特征），CART算法为二叉树。

信息增益

衡量一个集合中样本纯度的一种指标是信息熵，假设集合D中有K个类： $$Ent(D)= -\sum_{k=1}^K p_klog_2p_k$$

熵越大，数据越混乱，纯度越小。 决策树希望划分之后能减小熵，也就是划分前后之差越大越好，因此用信息增益来表示。假设样本集合D，属性a有V个可能取值，$D^v$表示属性a取值为v的样本子集，则有信息增益： $$Gain(D,a)=Ent(D) - \sum_{v=1}^V \frac {|D^v|}{|D|}Ent(D^v)$$

对所有属性，遍历计算每一个的信息增益，挑选最大的作为最优划分属性。这是ID3算法的选择方法。

信息增益比

考虑到信息增益会偏向取值较多的属性，因此C4.5算法引入信息增益比： $$Gain_ratio(D,a) = \frac {Gain(D,a)}{IV(a)}$$ $$IV(a) = -\sum_{v=1}^{V}\frac {|D^v|}{|D|} log_2 \frac {|D^v|}{|D|}$$

基尼指数

基尼指数表示集合的不确定性，CART决策树在分类时使用基尼指数最小的属性作为最优划分属性。 $$Gini(D)=\sum_{k=1}^K p_k(1-p_k) = 1 - \sum_{k=1}^K p_k^2$$ 考虑属性a的V种取值,则有： $$Gini(D,a) = \sum_{v=1}^V \frac {|D^v|}{|D|}Gini(D^v)$$

连续值

以上只考虑了属性是离散的，实际数据往往有连续的属性值。对于连续值，可以选择一个切分点，小于切分点的为一类，大于切分点的为另一类。切分点的可能选择为任意两个相邻属性值的平均值$\frac {a_i + a_{i+1}}2$。遍历所有可能的切分点，同样用信息增益（比）来决定最优切分点。

缺失值

实际数据集中，有的样本在某些属性上的数据会缺失。先给每个样本分配一个权重$w_i$,令$r_v=\frac {\sum_{\tilde{D}^v} w_i} {\sum_{D}wi}$ ，即某属性无缺失且取值为v的样本权重和/所有样本权重和

在选择划分属性时，只要考虑该属性不缺失的样本子集。 若某个样本在划分属性上数据缺失，将样本同时划入所有子节点，改变权重为$r_vw_i$。从概率论的角度来说，将一个样本以不同概率划入不同节点。

最小二乘回归树

决策树可以处理回归问题，即输出一个值而不是分类，核心思想是最小二乘法。对于每个切分变量j和切分点s,集合D可以被切分成两个子集R1,R2，相应的样本平均值为c1,c2。遍历所有属性j，每个属性可以求解切分点s,用下式选择最优切分(j,s)： $$min[\sum_{x_i\in R_1}(y_i-c_1)^2 + \sum_{x_i\in R_2}(y_i-c_2)^2]$$ 每个节点的输出值就是该节点中所有样本的平均值。

剪枝

决策树的生成是不断递归的直到不能继续分裂，意味着对训练数据拟合的好而泛化能力弱，因此通过剪枝的方法来简化决策树，相当于正则化，增强模型的泛化能力。

剪枝时考虑决策树的整体代价函数。设叶子节点个树为$|T|$，每个叶子节点t有属于k类的$N_{tk}$个样本，则代价函数为： $$C(T) = \sum_{t=1}^{|T|}N_tH_t(T) + \alpha|T|$$ $$H_t(T) = -\sum_{k}\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}$$

代价函数结合了训练数据的误差和决策树的复杂度，常数$\alpha$控制两者的trade off。 剪枝即最小化代价函数，由底向上，考虑去掉每个叶子节点能否降低代价函数值，直到代价函数不能再减小。

多变量决策树

上述决策树模型都只考虑切分单个属性，这样的结果是决策边界都是平行于坐标轴的。如果要有斜的决策边界，就要考虑多变量决策树，即候选切分属性要加入属性的线性组合。