支持向量机(Support Vector Machine,SVM)是一种分类算法,基本模型是定义在特征空间上的间隔最大的线性分类器,即在特征空间中寻找一个超平面来正确划分数据集,并使得样本点到超平面的距离最大化。
如果数据集线性可分的话,那有无数多个超平面可以将数据集正确分类。而支持向量机是要找到一个能将间隔最大化的超平面,因此解是唯一的,而且能尽可能的把不同类的数据点“分得更远”,使分类器泛化能力更强。
在样本空间内,划分超平面可以用一个线性方程表示,w和b为超平面的参数:
那么对于所有的数据点,都满足:
$$ \begin{cases}
w^Tx_i+b\ge 1, & y_i = 1 \
w^Tx_i+b\le -1, & y_i = -1
\end{cases}
$$
写成一个式子,即:
综上,要使间隔最大化,即:
如果数据集在样本空间内线性不可分,可以转化到更高维的某个特征空间Z,在Z中线性可分,所以支持向量机可以是一个非线性分类器。
假设样本空间为2维,即$x = (x_1, x_2)$,此时线性不可分,进行二阶转化到Z空间:$$z = \phi_2(x) = f(1,x_1,x_2,x_1^2,x_1x_2,x_2^2)$$
此时Z空间是6维空间,如果是更高阶的转化,会使特征空间的维度迅速上升,导致上述二次规划问题的复杂度非常高。如果用高斯核函数,特征空间甚至为无限维。因此,引入拉格朗日对偶问题,使算法复杂度与特征空间维度无关,而与样本数量相关。
对于支持向量机的基本形式的每个约束引入非负的拉格朗日乘子$\alpha_i$,构造拉格朗日函数:
易得: $$\begin{eqnarray} w&=&\sum_{i=1}^n \alpha_i y_i x_i\ 0&=&\sum_{i=1}^n \alpha_i y_i \end{eqnarray}$$ 代回拉格朗日函数并展开,可以把支持向量机的求解转换为不等式约束的最优化问题,也就是原问题的对偶问题,详细数学证明参考台大机器学习技法:
然后根据$$w=\sum_{i=1}^n \alpha_i y_i x_i$$可以计算出w
根据KKT条件,最优解必须满足:
因此,对于所有支持向量,满足$|w^Tx+b|=1$,自然满足KKT条件;对于其他样本点,有$|w^Tx+b|>1$,要满足KKT条件,则对应的拉格朗日乘子$\alpha_i=0$
计算b时,考虑所有$\alpha_i>0$的样本(必定是支持向量),得到$b=y_n-w^Tx$。理论上用一个样本就可以计算出b,实际上往往用所有可能的样本计算出b再求平均。
上文提到,当在样本空间$X\in R^d$中数据集线性不可分时,总是可以转化到高维的特征空间$Z\in R^\tilde{d}$中,使数据集在Z空间中线性可分。
此时,假设X到Z空间的映射为$\phi(x)$,在Z空间中解SVM对偶问题时,需要计算两个样本的内积$z^T\acute{z}$,也就是$\phi(x)^T\acute{\phi(x)}$。特征空间的维度$\tilde{d}$往往很高,甚至是无限维,计算内积的时间复杂度$O(\tilde{d})$很大。为了避免在Z空间计算内积,使用核函数$K(x,\acute{x})$在X空间内直接计算,时间复杂度为$O(d)$。
举例说明,假设X空间维度为d,则$x=(x_1,x_2,...,x_d)$,使用2阶非线性变换$$\phi_2(x)=f(1,x_1,x_2,...,x_d,x_1^2,x_1x_2,...,x_1x_d,...,x_d^2)$$ Z空间内积:
显然,这样计算的话可以只用X空间内的内积$x^T\acute{x}$来表示Z空间的内积,核函数为
一个函数能$K(x_i,x_j)$作为核函数的充要条件是:对任意x,满足矩阵$[K(x_i,x_j)]_{n*n}$是半正定矩阵。详细证明参考李航的《统计学习方法》
常用的核函数
- 线性核$K(x_i,x_j)=x_i^Tx_j$ 只能处理线性可分数据,计算快
- 多项式核$K(x_i,x_j)=(\xi+\gamma x_i^Tx_j)^Q$ 能处理线性不可分数据,可以控制阶数Q,计算量大,参数$(\xi,\gamma,Q)$选择困难
- 高斯核$K(x_i,x_j)=e^{-\frac{||x_i-x_j||^2}{2\sigma^2}}$ 特征空间无限维,非常强大,只有一个参数;计算速度比线性核慢,相对容易过拟合。因为高斯函数的形状,高斯核函数又被称为Radial Basis Function(RBF)核函数
高斯核例子:
其中$\phi(x)=e^{-x^2}\sum_{i=0}^{\infty}\sqrt\frac{2^i}{i!}x^i$,将d维的样本空间映射到了无限维的特征空间。
之前只考虑线性可分的数据,想要把每个样本都正确分类,这样容易造成过拟合。如果允许错误分类,就有了软间隔(soft-margin)支持向量机。
用$\xi$表示分类错误的大小,$\xi_n=max(1-y_n(w^Tz_n+b), 0)$,再用常数C表示对错误的容忍度,则可以写出软间隔支持向量机的表达式:
考虑软间隔支持向量机的对偶问题,构造拉格朗日函数:
对于这个二次规划问题,KKT条件变成:
对于任意一个样本,如果$\alpha_i=0$, 则不是支持向量,跟计算w,b无关;如果$\alpha_i>0$,且$\alpha_i<C$,则$\xi_i=0$,此样本为支持向量,落在决策边界上,根据$y_i(w^Tx_i+b)-1+\xi_i=0$可以计算出b;如果$\alpha_i=C$,则$\xi_i>0$,即此样本越过了决策边界,如果误差大可能被错误分类。
软间隔支持向量机中,参数C越大,则越不能容忍错误,模型更强大也更容易出现过拟合。
如果一个SVM模型的支持向量很多,说明有很多样本处于决策边界上甚至误分类,这个模型可能就不太好。
从损失函数的角度考虑,软间隔支持向量机的原始问题
整体可以看作一个损失函数,分类错误的大小$\xi_n=max(1-y_n(w^Tz_n+b), 0)$,用函数表示的话是合页损失函数(hinge loss)。
SVM最终可以转化成一个二次规划问题,但是这个二次规划问题的求解效率与样本的数量有关。SMO(sequential minimal optimization)算法能够高效求解SVM二次规划问题。
SMO算法的基本思路是:如果所有变量的解都满足最优化问题的KKT条件,则此问题的解就得到了。否则,选择两个变量,固定其他变量,对这两个变量构建一个二次规划问题,可以通过解析方法求解,使这两个变量的解逼近原问题的解。不断迭代,求解原问题。
因为条件$\sum_{i=1}^n \alpha_i y_i=0$,如果确定一个变量,则另一个变量也就确定了:$$\alpha_1y_i+\alpha_2y_2=C$$
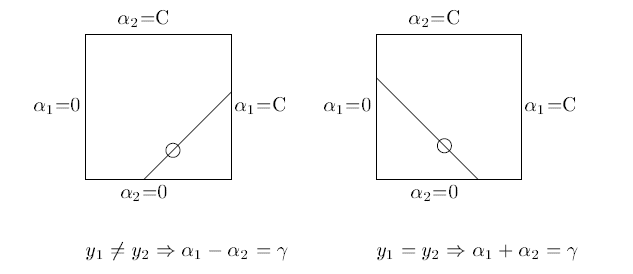
在选择两个待更新变量时,首先找一个违反KKT条件最严重的变量。确定第二个变量时采用启发式算法,选择两个差别很大的变量,会带来更大的优化效果。定义偏差$E_i = max(y_i(w^Tx_i+b)-1, 0)$,确定$\alpha_1$后找到使$|E_1 - E_2|$最大的$\alpha_2$。
