- 文章、观点
- 阅读、编辑、回顾历史、工具(来自:维基百科混沌理论翻译)
注:值r=28,σ=10,b=8/3的洛伦兹吸引子的一个图
注:一个显示混沌行为的中间能量的双杆摆的动画。从一个稍微不同的初始条件启动钟摆将导致一个截然不同的轨迹。双杆摆是具有混沌解的最简单动力系统之一。以下是双摆的方程:
其中,$\theta_1$ 与 ode45 函数求解双摆的方程。下面的代码片段展示了如何使用 ode45 函数来解决双摆问题,并绘制出摆的运动轨迹。
混沌理论是一个跨学科的科学研究领域和数学分支,专注于对初始条件高度敏感的动力系统的基本模式和确定性定律,曾被认为具有完全随机的无序和不规则状态。混沌理论指出,在混沌复杂系统的表面随机性中,存在潜在的模式、互连、恒定反馈回路、重复、自相似、分形和自组织。蝴蝶效应是混沌的一个基本原理,它描述了确定性非线性系统一个状态的微小变化如何导致后期状态的巨大差异(这意味着对初始条件有敏感的依赖性)。这种行为的一个比喻是,在巴西扇动翅膀的蝴蝶可能会在德克萨斯州引发龙卷风。
初始条件的微小差异,例如由于测量误差或数值计算中的舍入误差引起的差异,可能会对此类动力系统产生广泛的分歧结果,使其行为的长期预测通常不可能实现。即使这些系统是确定性的,这也可能发生,这意味着它们未来的行为遵循独特的进化,完全由它们的初始条件决定,不涉及随机因素。换句话说,这些系统的确定性并不能使它们成为可预测的。这种行为被称为确定性混沌,或者简称为混沌。爱德华·洛伦茨将这一理论总结为:
混沌:当现在决定了未来,但大致的现在并不能大致决定未来。
混沌行为存在于许多自然系统中,包括流体流动、心跳不规则、天气和气候。它也会自发地出现在一些带有人工组件的系统中,例如道路交通。这种行为可以通过混沌数学模型的分析来研究,也可以通过递推图和庞加莱映射等分析技术来研究。混沌理论应用于多个学科,包括气象学、人类学、社会学、环境科学、计算机科学、工程、经济学、生态学和流行病危机管理。该理论为复杂动力系统、混沌边缘理论和自组装过程等研究领域奠定了基础。
混沌理论涉及确定性系统,其行为原则上可以预测。混沌系统在一段时间内是可预测的,然后“出现”成为随机的。混沌系统的行为可以有效预测的时间取决于三件事:预测中可以容忍多少不确定性,测量其当前状态的准确性,以及取决于系统动力学的时间尺度,称为李雅普诺夫时间。李雅普诺夫时间的一些例子是:混沌电路,大约1毫秒;天气系统,几天(未经证实);太阳系内部,400万至500万年。在混沌系统中,预测的不确定性随着时间的推移呈指数级增加。因此,从数学上讲,将预测时间增加一倍比预测中的比例不确定性增加一倍还要多。这意味着,在实践中,无法在超过李雅普诺夫时间两到三倍的区间内做出有意义的预测。当无法做出有意义的预测时,系统会出现随机现象。
混沌理论是一种定性和定量分析的方法,用于研究动态系统的行为,这些行为不能用单一的数据关系来解释和预测,而必须用完整、连续的数据关系进行解释和预测。
注:此图由x → 4 x (1 – x) and y → (x + y) mod 1显示对初始x位置的灵敏度。这里,两个系列的x和y值随着时间的推移从微小的初始差异显著偏离。
在通常的用法中,“混乱”的意思是“混乱的状态”。然而,在混沌理论中,这个术语的定义更为精确。尽管不存在普遍接受的混沌数学定义,但最初由Robert L.Devaney提出的一个常用定义认为,要将动力系统归类为混沌,它必须具有以下性质:
1.它必须对初始条件敏感,
2.它必须是拓扑传递的,
3.它必须是致密的。
在某些情况下,上面的最后两个性质实际上意味着对初始条件的敏感性。在离散时间的情况下,这对于度量空间上的所有连续映射都是正确的。在这些情况下,虽然它通常是最具实际意义的性质,但“对初始条件的敏感性”无需在定义中说明。
如果注意力仅限于区间,则第二个性质意味着另外两个。混沌的另一种通常较弱的定义只使用上面列表中的前两个属性。
主要文章:蝴蝶效应
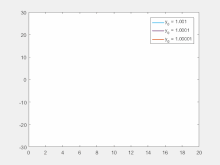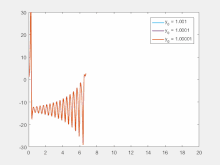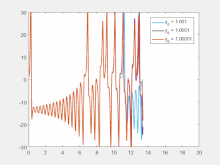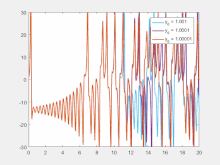
注:洛伦兹方程用于生成y变量的图。x和z的初始条件保持不变,但y的初始条件在1.001、1.0001和1.00001之间变化。ρ、σ和β的值分别为45.92、16和4。从图中可以看出,在这三种情况下,即使初始值的最微小差异也会在大约12秒的进化后引起显著变化。这是对初始条件敏感依赖的一个例子。
对初始条件的敏感性意味着混沌系统中的每个点都被具有显著不同的未来路径或轨迹的其他点任意近似。因此,当前轨迹的任意小的变化或扰动可能导致显著不同的未来行为。
对初始条件的敏感性通常被称为“蝴蝶效应”,这是因为爱德华·洛伦茨1972年在华盛顿特区给美国科学促进会的一篇论文的标题,题为“可预测性:巴西的蝴蝶翅膀扇动会在德克萨斯州引发龙卷风吗?”。扑翼代表了系统初始条件的一个小变化,这导致了一系列事件,阻碍了大规模现象的可预测性。如果蝴蝶没有扇动翅膀,整个系统的轨迹可能会大不相同。
正如洛伦茨1993年出版的题为《混沌的本质》的书中所建议的那样,“敏感依赖可以作为混沌的一个可接受的定义”。在同一本书中,洛伦茨将蝴蝶效应定义为:“动力系统状态的微小变化将导致随后的状态与没有变化的状态大不相同。”上述定义与解对初始条件的敏感依赖性(SDIC)是一致的。开发了一个理想化的滑雪模型来说明时变路径对初始位置的敏感性。可预测性水平可以在SDIC开始之前(即,在初始附近轨迹的显著分离之前)确定。
对初始条件敏感的一个后果是,如果我们从关于系统的有限信息开始(就像实践中通常的情况一样),那么超过一定时间,系统将不再是可预测的。这在天气方面最为普遍,通常只有大约一周的时间可以预测。这并不意味着人们不能对遥远的未来事件断言任何东西,只意味着对系统存在一些限制。例如,我们知道地球表面的温度不会自然达到100°C(212°F)或低于100°C负极130摄氏度(负极202°F)(在当前地质时代),但我们无法准确预测哪一天的气温将是一年中最热的。
在更多的数学术语中,李雅普诺夫指数以与扰动初始条件的指数发散率的形式测量对初始条件的灵敏度。更具体地说,给定相空间中无限接近的两个起始轨迹,具有初始分离
其中t是时间,λ是李雅普诺夫指数。分离速率取决于初始分离向量的方向,因此可以存在李雅普诺夫指数的整个谱。李雅普诺夫指数的数量等于相空间的维数,尽管通常只指最大的一个。例如,最大李雅普诺夫指数(MLE)最常被使用,因为它决定了系统的整体可预测性。正的MLE通常被视为系统是混沌的指示。
除了上述性质外,还存在与初始条件灵敏度有关的其他性质。例如,这些包括测量理论混合(如遍历理论中所讨论的)和K系统的性质。
混沌系统可能具有进化变量的值序列,这些值序列精确地重复自身,从该序列中的任何点开始给出周期性行为。然而,这种周期序列是排斥的,而不是吸引的,这意味着如果进化变量在序列之外,无论多么接近,它都不会进入序列,事实上,它会偏离序列。因此,对于几乎所有的初始条件,变量都以非周期行为无序演化。
注:一组状态[x,y]的六次迭代通过逻辑图。第一个迭代(蓝色)是初始条件,基本上形成一个圆。动画显示循环初始条件的第一次到第六次迭代。可以看出,混合发生在我们迭代的过程中。第六次迭代表明,这些点几乎完全分散在相空间中。如果我们在迭代中取得进一步的进展,混合将是均匀和不可逆转的。此逻辑图有关系式



注:地图由x定义→ 4x(1–x)和y→ (x+y) mod 1也显示了拓扑混合。在这里,蓝色区域通过动力学首先转换为紫色区域,然后转换为粉色和红色区域,最后转换为散布在空间中的垂直线云。
拓扑混合(或拓扑传递性的较弱条件)意味着系统随着时间的推移而演化,使得其相空间的任何给定区域或开集最终与任何其他给定区域重叠。这种“混合”的数学概念对应于标准直觉,有色染料或流体的混合是混沌系统的一个例子。
拓扑混合经常被省略在对混沌的流行描述中,这些描述将混沌等同于只对初始条件敏感。然而,仅仅对初始条件的敏感依赖并不能产生混乱。例如,考虑一个简单的动力系统,它是由一个初始值重复加倍产生的。这个系统对任何地方的初始条件都有敏感的依赖性,因为任何一对附近的点最终都会被广泛分离。然而,这个例子没有拓扑混合,因此没有混沌。事实上,它有着极其简单的行为:除了0之外的所有点都趋向于正或负无穷大。
一个图 f:X→X 被认为是拓扑传递的,如果对于任何一对非空的开集

一个重要的相关定理是Birkhoff传递性定理。很容易看出,稠密轨道的存在意味着拓扑传递性。Birkhoff传递性定理指出,如果X是第二个可数的完全度量空间,则拓扑传递性意味着X中存在具有稠密轨道的稠密点集。
混沌系统具有稠密的周期轨道意味着空间中的每个点都被周期轨道任意接近。由x定义的一维逻辑映射→ 4x(1–x)是具有周期轨道密度的最简单系统之一。例如,5−58


Sharkovskii定理是Li和Yorke(1975)证明的基础,即任何连续的一维系统,只要表现出周期为三的规则循环,也会表现出每隔一个长度的规则循环以及完全混沌的轨道。
注:洛伦兹吸引子表现出混沌行为。这两个图显示了在吸引子占据的相空间区域内对初始条件的敏感依赖性。
一些动力学系统,比如一维逻辑映射由x→ 4x(1–x)所定义,在任何地方都是混沌的,但在许多情况下,混沌行为仅在相空间的子集中发现。当混沌行为发生在吸引子上时,最令人感兴趣的情况就会出现,因为从那时起,一大组初始条件会导致轨道收敛到这个混沌区域。
可视化混沌吸引子的一个简单方法是从吸引子吸引池中的一个点开始,然后简单地绘制其后续轨道。由于拓扑传递性条件,这很可能会产生整个最终吸引子的图片,事实上,右图中显示的两个轨道都给出了洛伦兹吸引子的一般形状的图片。这个吸引子来自洛伦兹天气系统的一个简单的三维模型。洛伦兹吸引子可能是最著名的混沌系统图之一,可能是因为它不仅是第一个混沌系统图,也是最复杂的混沌系统图之一,因此产生了一个非常有趣的模式,只需一点想象力,它看起来就像蝴蝶的翅膀。
与定点吸引子和极限环不同,混沌系统中产生的吸引子,即奇异吸引子,具有很大的细节和复杂性。奇异吸引子出现在连续动力系统(如洛伦兹系统)和一些离散系统(如Hénon映射)中。其他离散动力系统有一个称为Julia集的排斥结构,它形成于不动点吸引盆地之间的边界。朱莉娅套装可以被认为是奇怪的排斥者。奇异吸引子和Julia集通常都具有分形结构,并且可以为它们计算分形维数。
注:广义洛伦兹模型中混沌和非混沌吸引子共存。有128个不同颜色的轨道,从不同的初始条件开始,无量纲时间在0.625到5之间,加热参数r=680。混沌轨道反复返回到原点的鞍点附近。非混沌轨道最终接近两个稳定临界点中的一个,如蓝色大点所示。混沌轨道和非混沌轨道在相空间中占据不同的吸引区域。
与单一类型的混沌解相比,最近使用洛伦兹模型的研究强调了考虑各种类型的解的重要性。例如,使用相同的建模配置但不同的初始条件,共存的混沌和非混沌可能出现在相同的模型(例如,双摆系统)中。从经典和广义洛伦兹模型中获得的吸引子共存的发现,提出了一种修正的观点,即“整个天气具有混沌和秩序的双重性质,具有明显的可预测性”,而不是传统的“天气是混沌的”观点。
注:逻辑分叉图x→ r*x(1–x)。每个垂直切片显示特定r值的吸引子。该图显示随着r的增加周期加倍,最终产生混沌。更频繁地访问较暗的点。
离散混沌系统,如逻辑映射,无论其维度如何,都可能表现出奇怪的吸引子。具有抛物极大值和费根鲍姆常数的一维映射的普遍性

相反,对于连续动力系统,Poincaré–Bendixson定理表明,一个奇怪的吸引子只能出现在三维或三维以上。有限维线性系统从来都不是混沌的;一个动力系统要表现出混沌行为,就必须是非线性的。
Poincaré–Bendixson定理指出,二维微分方程具有非常规则的行为。下面讨论的洛伦兹吸引子是由三个微分方程组生成的,例如:
其中x、y和z组成系统状态,t是时间,σ、ρ、β是系统参数。右边的五项是线性的,而两项是二次的;总共七个学期。另一个著名的混沌吸引子是由Rössler方程产生的,该方程在七个非线性项中只有一个。斯普洛特发现了一个只有五项的三维系统,它只有一个非线性项,对于某些参数值,它表现出混沌。张和海德尔证明,至少对于耗散和保守的二次系统,右手边只有三到四项的三维二次系统不能表现出混沌行为。简单地说,原因是这类系统的解是渐近于二维曲面的,因此解表现良好。
虽然Poincaré–Bendixson定理表明欧几里得平面上的连续动力系统不可能是混沌的,但具有非欧几里得几何的二维连续系统可以表现出混沌行为。自行发布的来源?也许令人惊讶的是,混沌也可能发生在线性系统中,只要它们是无限维的。线性混沌理论是数学分析的一个分支,被称为函数分析。
上述三个常微分方程的优雅集合被称为三维洛伦兹模型。自1963年以来,在许多研究中开发了更高维的洛伦兹模型,用于检验非线性程度增加及其与加热和耗散的集体效应对溶液稳定性的影响。
耦合离散映射的直接推广基于卷积积分,该积分介导空间分布映射之间的相互作用:
其中,内核
![{\displaystyle f[\psi _{n}({\vec {r}},t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fa3ba17d6e2b56466d57d8b60a2e46ec4925b90)
![{\displaystyle \psi \rightarrow G\psi [1-\tanh(\psi )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fec62ff5ebcf9fac8e71b101d6d2da0ef37f2df2)
![{\displaystyle f[\psi ]=\psi ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331a4c25ef04f99d8d77f2be74bf1fa8a4ec21b2)



在物理学中,急动是位置相对于时间的三阶导数。因此,这种形式的微分方程
有时被称为jerk方程。研究表明,一个与三个一阶常非线性微分方程组等价的急动方程,在某种意义上是表现出混沌行为的解的最小设置。这激发了人们对急动系统的数学兴趣。涉及四阶或更高阶导数的系统相应地被称为超急动系统。
急动系统的行为由急动方程描述,对于某些急动方程,简单的电子电路可以对解进行建模。这些电路被称为急动电路。
急动电路最有趣的特性之一是混沌行为的可能性。事实上,某些众所周知的混沌系统,如洛伦兹吸引子和Rössler映射,通常被描述为三个一阶微分方程的系统,这些方程可以组合成一个(尽管相当复杂)急动方程。另一个例子具有x量级的非线性jerk方程是:
这里,A是一个可调参数。对于a=3/5,该方程具有混沌解,并且可以用以下急动电路来实现;所需的非线性是由两个二极管引起的:
在上述电路中,除了

类似的电路只需要一个二极管或者根本不需要二极管。
另见著名的蔡氏电路,混沌真随机数发生器的一个基础。该电路易于构建,使其成为现实世界中普遍存在的混沌系统的例子。
在适当的条件下,混沌自发地演变成一种步调一致的模式。在Kuramoto模型中,四个条件足以在混沌系统中产生同步。例子包括Christiaan Huygens钟摆、萤火虫、神经元的耦合振荡、伦敦千禧桥共振和约瑟夫逊结的大型阵列(Josephson junctions)
注:巴恩斯利蕨类(Barnsley fern)使用了混沌活动。自然形态(蕨类植物、云、山脉等)可以通过迭代函数系统(IFS)重新创建。
混沌理论的早期支持者是亨利·庞加莱(Henri Poincaré)。19世纪80年代,在研究三体问题时,他发现可能存在非周期性轨道,但不会永远增加或接近固定点。1898年,雅克·哈达玛发表了一篇关于自由粒子在恒定负曲率表面上无摩擦滑动的混沌运动的有影响力的研究,称为“哈达玛台球(Hadamard's billiards)”。Hadamard能够证明所有的轨迹都是不稳定的,因为所有粒子的轨迹彼此呈指数发散,具有正的李雅普诺夫指数。
混沌理论起源于遍历理论领域。后来, George David Birkhoff,Andrey Nikolaevich Kolmogorov,Mary Lucy Cartwright和 John Edensor Littlewood以及Stephen Smale也对非线性微分方程进行了研究。除了Smale,这些研究都直接受到物理学的启发:伯霍夫的三体问题,科尔莫戈罗夫的湍流和天文问题,以及卡特赖特和利特尔伍德的无线电工程。需要引用尽管尚未观察到混沌行星运动,但实验人员在没有理论解释他们所看到的情况的情况下,遇到了流体运动中的湍流和无线电电路中的非周期振荡。
尽管在20世纪上半叶有了初步的见解,但混沌理论直到本世纪中叶才正式化,当时一些科学家首次发现,当时流行的系统理论线性理论根本无法解释某些实验的观测行为,比如逻辑图。混沌理论家认为,测量的不精确性和简单的“噪声”是所研究系统的完整组成部分。1959年,鲍里斯·瓦列里亚诺维奇·奇里科夫提出了哈密顿系统中经典混沌出现的一个准则(奇里科夫准则 Chirikov criterion)。他用这个标准解释了开放镜阱中等离子体约束的一些实验结果。这被认为是混沌的第一个物理理论,它成功地解释了一个具体的实验。鲍里斯·奇里科夫本人被认为是经典和量子混沌的先驱。
电子计算机是混沌理论发展的主要催化剂。混沌理论的许多数学都涉及简单数学公式的重复迭代,这用手是不切实际的。电子计算机使这些重复计算变得实用,而图形和图像使这些系统可视化成为可能。1961年11月27日,作为京都大学Chihiro Hayashi实验室的一名研究生,上田义辅正在用模拟计算机进行实验,并注意到了他所说的“随机过渡现象”。然而,他的顾问当时并不同意他的结论,直到1970年才允许他报告他的发现。
注:机翼尖端涡流中的湍流。对系统产生湍流的临界点的研究对混沌理论很重要,例如由苏联物理学家列夫·兰道分析,他发展了兰道-霍普夫湍流理论。David Ruelle和Floris Takens后来预测,流体湍流可能通过一个奇怪的吸引子发展,这是混沌理论的主要概念。
爱德华·洛伦茨(Edward Lorenz)是这一理论的早期先驱。1961年,他在天气预报方面的工作偶然引起了他对混乱的兴趣。洛伦茨和他的合作者Ellen Fetter使用一台简单的数字计算机,一台皇家McBee LGP-30,进行天气模拟。他们想再次看到一系列数据,为了节省时间,他们在中途开始了模拟。他们通过输入与原始模拟中间条件相对应的数据打印输出来实现这一点。令他们惊讶的是,机器开始预测的天气与之前的计算完全不同。他们追踪到了电脑打印的结果。计算机的工作精度为6位数,但打印输出的变量四舍五入为3位数,因此像0.506127这样的值打印为0.506。这种差异很小,当时的共识是它不应该产生实际效果。然而,洛伦茨发现,初始条件的微小变化会导致长期结果的巨大变化。洛伦茨的发现,也就是洛伦茨吸引器的名字,表明即使是详细的大气建模,通常也无法做出准确的长期天气预测。
1963年,Benoit Mandelbrot研究信息理论,发现噪音在许多现象中(包括股票价格和电话)都像康托尔集一样,一组具有无限粗糙度和细节的点Mandelbrot描述了“诺亚效应”(其中可能发生突然的不连续变化)和“约瑟夫效应”(在这种情况下,一个值可能会持续一段时间,但之后会突然改变)。1967年,他发表了《英国海岸有多长?统计自相似性和分数维》,表明海岸线的长度随着测量仪器的刻度而变化,在所有刻度上都相似,对于一个无限小的测量设备来说,长度是无限的。他认为,从远处看(0维),从相当近的地方看(3维),麻线球看起来像一个点,或者弯曲的线(1维),他认为物体的尺寸相对于观察者是相对的,可能是分数的。一个物体的不规则性在不同的尺度上是恒定的(“自相似性”)是一个分形(例如Menger海绵、Sierpiński垫圈和Koch曲线或雪花,它无限长,但包围着有限的空间,具有分形维数。1982年,Mandelbrot出版了《自然的分形几何》,成为混沌理论的经典。)。
1977年12月,纽约科学院组织了第一次关于混沌的研讨会,出席者有David Ruelle、Robert May、James A.Yorke(数学中“混沌”一词的创造者)、Robert Shaw和气象学家Edward Lorenz。第二年,Pierre Coullet和Charles Tresser发表了《自同态与再规范化组》,Mitchell Feigenbaum的文章《一类非线性变换的定量普遍性》在被裁判驳回3年后终于发表在期刊上。因此,Feigenbaum(1975)和Coullet&Tresser(1978)发现了混沌的普遍性,允许将混沌理论应用于许多不同的现象。
1979年,在Pierre Hohenberg在阿斯彭组织的一次研讨会上,Albert J.Libchaber介绍了他对瑞利-贝纳德对流系统中导致混乱和湍流的分叉级联的实验观察。1986年,他与Mitchell J.Feigenbaum一起因其鼓舞人心的成就而获得沃尔夫物理学奖。
1986年,纽约科学院与美国国家心理健康研究所和海军研究办公室共同组织了第一次关于生物学和医学混乱的重要会议。在那里,BernardoHuberman提出了一个精神分裂症患者眼睛追踪功能障碍的数学模型。这导致了20世纪80年代通过混沌理论的应用,例如在病理心动周期的研究中,生理学的更新。
1987年,Per-Bak、Chao Tang和Kurt Wiesenfeld在《物理评论快报》上发表了一篇论文,首次描述了自组织临界(SOC),它被认为是自然界中复杂性产生的机制之一。
除了主要基于实验室的方法,如Bak–Tang–Wiesenfeld沙堆,许多其他研究都集中在已知(或怀疑)显示尺度不变行为的大规模自然或社会系统上。尽管这些方法并不总是受到所研究主题专家的欢迎(至少在最初是这样),但SOC已被确定为解释许多自然现象的有力候选者,包括地震、,(早在SOC被发现之前,就被认为是尺度不变行为的来源,如古腾堡-里希特定律(Gutenberg–Richter_law)描述地震规模的统计分布,以及描述余震频率的大森定律)、太阳耀斑、金融市场等经济系统的波动(SOC在经济学中很常见)、景观形成、森林火灾、山体滑坡、流行病,以及生物进化(例如,SOC被称为Niles Eldredge和Stephen Jay Gould提出的“间断平衡”理论背后的动力机制)。考虑到事件规模的无标度分布的影响,一些研究人员认为,另一个应该被视为SOC例子的现象是战争的发生。SOC的这些研究包括建模尝试(开发新模型或根据给定自然系统的具体情况调整现有模型)和广泛的数据分析,以确定自然比例定律的存在和/或特征。
同年,詹姆斯·格里克出版了《混沌:创造新科学》,成为畅销书,并向广大公众介绍了混沌理论的一般原理及其历史。混沌理论最初是少数孤立个体的领域,后来逐渐成为一门跨学科和制度学科,主要以非线性系统分析的名义出现。引用托马斯·库恩在《科学革命的结构》(1962)中提出的范式转变概念,许多“混沌学家”(正如一些人所描述的那样)声称这一新理论就是这种转变的一个例子,格里克支持这一论点。
更便宜、更强大的计算机的出现拓宽了混沌理论的适用范围。目前,混沌理论仍然是一个活跃的研究领域,涉及许多不同的学科,如数学、拓扑、物理学、社会系统、人口建模、生物学、气象学、天体物理学、信息论、计算神经科学、流行病危机管理等。
对初始条件的敏感依赖(即蝴蝶效应)已通过以下民间传说进行了说明:
丢失一个钉子,坏了一只蹄铁;坏了一只蹄铁,折了一匹战马;折了一匹战马,伤了一位骑士;杀了一位骑士,输了一场战斗;输了一场战斗,亡了一个帝国。而这一切都是因为缺少一颗马蹄钉。
基于上述,许多人错误地认为,微小的初始扰动的影响随着时间单调增加,任何微小的扰动最终都会对数值积分产生巨大影响。然而,在2008年,洛伦茨表示,他不认为这首诗描述了真正的混乱,但它更好地说明了更简单的不稳定现象,这首诗隐含地表明,随后的小事件不会逆转结果(洛伦茨,2008)。根据分析,这首诗只是表示分歧,而不是有界性。有界性对于蝴蝶图案的有限尺寸是很重要的。在最近的一项研究中,上述诗句的特征最近被表示为“有限的时间敏感依赖性”。
注:一个圆锥纺织外壳,外观类似于规则30,是一个具有混沌行为的元胞自动机。
尽管混沌理论是从观测天气模式中诞生的,但它已经适用于各种其他情况。今天受益于混沌理论的一些领域是地质学、数学、生物学、计算机科学、经济学、金融学、气象学、哲学、人类学、物理学、政治学、人口动力学和机器人学。下面列出了一些类别和示例,但这绝不是一个全面的列表,因为新的应用程序正在出现。
混沌理论在密码学中已经应用了很多年。在过去的几十年里,混沌和非线性动力学已经被用于数百个密码原语的设计。这些算法包括图像加密算法、散列函数、安全伪随机数生成器、流密码、水印和隐写术。这些算法大多基于单模态混沌映射,其中很大一部分算法以混沌映射的控制参数和初始条件为关键。从更广泛的角度来看,在不失一般性的情况下,混沌映射和密码系统之间的相似性是设计基于混沌的密码算法的主要动机。一种类型的加密,秘密密钥或对称密钥,依赖于扩散和混淆,混沌理论对其进行了很好的建模。另一种类型的计算,DNA计算,当与混沌理论相结合时,提供了一种加密图像和其他信息的方法。许多DNA混沌密码算法被证明要么不安全,要么所应用的技术被认为是无效的。
机器人学是最近受益于混沌理论的另一个领域。机器人不再以试错式的精细化方式与环境互动,而是使用混沌理论来建立预测模型。被动行走的两足机器人表现出了混沌动力学。
一百多年来,生物学家一直在用种群模型追踪不同物种的种群。大多数模型都是连续的,但最近科学家已经能够在某些群体中实现混沌模型。例如,一项对加拿大山猫模型的研究表明,在种群增长中存在混乱行为。混沌也可以在生态系统中发现,例如水文。尽管水文的混沌模型有其缺点,但从混沌理论的角度来看数据仍有很多需要学习的地方。另一个生物学应用是在心胎记术中发现的。胎儿监护是在获得准确信息的同时尽可能做到无创的微妙平衡。通过混沌建模可以获得胎儿缺氧警告信号的更好模型。
正如Perry所指出的,生态学中混沌时间序列的建模有助于约束。区分真正的混沌和仅存在于模型中的混沌总是存在潜在的困难。因此,模型中的约束和/或用于比较的重复时间序列数据将有助于将模型约束为接近现实的东西,例如Perry&Wall 1984。基因对基因协同进化有时在等位基因频率上表现出混乱的动力学。添加变量夸大了这一点:混沌在包含额外变量以反映真实人口的额外方面的模型中更为常见。罗伯特·M·梅自己做了一些基础性的作物共同进化研究,这反过来又帮助塑造了整个领域。即使在稳定的环境中,仅仅将一种作物和一种病原体结合起来,也可能导致病原体种群的准周期性或混沌性振荡。
通过应用混沌理论也有可能改进经济模型,但预测经济系统的健康状况以及哪些因素对其影响最大是一项极其复杂的任务。经济和金融系统与经典自然科学中的系统有根本不同,因为前者本质上是随机的,因为它们是人与人之间相互作用的结果,因此纯确定性模型不太可能提供数据的准确表示。在经济学和金融学中测试混沌的实证文献给出了非常复杂的结果,部分原因是对混沌的具体测试和对非线性关系的更一般的测试之间的混淆。
通过递归量化分析可以发现经济学中的混沌现象。事实上,Orlando等人通过所谓的递推量化相关指数能够检测出时间序列中隐藏的变化。然后,使用相同的技术来检测从层流(规则)到湍流(混沌)阶段的转变,以及宏观经济变量之间的差异,并突出经济动力学的隐藏特征。最后,混沌理论有助于建模经济如何运行,以及嵌入新冠肺炎等外部事件造成的冲击。
在化学中,预测气体溶解度对于制造聚合物至关重要,但使用粒子群优化(PSO)的模型往往会收敛到错误的点。PSO的改进版本是通过引入混沌来创建的,这可以防止模拟陷入困境。在天体力学中,尤其是在观测小行星时,应用混沌理论可以更好地预测这些物体何时接近地球和其他行星。冥王星的五颗卫星中有四颗是无序旋转的。在量子物理和电气工程中,对约瑟夫逊结大阵列的研究得益于混沌理论。在离家较近的地方,煤矿一直是危险的地方,经常发生的天然气泄漏导致许多人死亡。直到最近,还没有可靠的方法来预测它们何时会发生。但这些气体泄漏具有混乱的趋势,如果建模得当,可以相当准确地预测。
混沌理论可以应用于自然科学之外,但从历史上看,几乎所有此类研究都缺乏再现性;外部有效性差;和/或忽视交叉验证,导致预测准确性差(如果甚至尝试了样本外预测)。Glass、Mandell和Selz发现,目前还没有任何脑电图研究表明存在奇怪的引诱物或其他混乱行为的迹象。
研究人员继续将混沌理论应用于心理学。例如,在对群体行为进行建模时,异质成员的行为可能会像在不同程度上共享Wilfred Bion理论中的一个基本假设一样,研究人员发现,群体动态是成员个体动态的结果:每个个体以不同的尺度再现群体动态,并且群体的混乱行为反映在每个成员身上。
Redington和Reidbord(1992)试图证明人类的心脏可以表现出混乱的特征。他们监测了一名心理治疗患者在治疗过程中经历不同情绪强度时期时心跳间隔的变化。结果不可否认是不确定的。作者不仅在据称显示混沌动力学证据的各种图(谱分析、相位轨迹和自相关图)中存在歧义,而且当他们试图计算李雅普诺夫指数作为对混沌行为的更明确确认时,作者发现他们不能可靠地做到这一点。
在1995年的论文中,梅特卡夫和艾伦坚持认为,他们在动物行为中发现了周期加倍导致混乱的模式。作者研究了一种众所周知的反应,即时间表诱导的多饮症,即在一定时间内被剥夺食物的动物在最后出现食物时会喝下不寻常的水。此处操作的控制参数(r)是进给之间的间隔长度,一旦恢复。作者谨慎地测试了大量的动物,并包括了许多复制品,他们设计了实验,以排除反应模式的变化是由r的不同起始位置引起的可能性。
时间序列和第一次延迟图为所提出的主张提供了最好的支持,显示出随着喂食时间的增加,从周期性到不规则性的过程相当明显。另一方面,各种相位轨迹图和频谱分析与其他图或整体理论的匹配不够好,无法不可避免地导致混沌诊断。例如,相位轨迹没有显示出朝着越来越大的复杂性(并且远离周期性)的明确进展;这个过程似乎相当混乱。此外,梅特卡夫和艾伦在他们的光谱图中看到了两个和六个周期,还有其他解释的空间。所有这些模糊性都需要一些曲折的事后解释,以表明结果符合混沌模型。
Amundson和Bright通过调整职业咨询模型,将对员工和就业市场之间关系的混乱解释纳入其中,发现可以为那些在职业决策中挣扎的人提供更好的建议。现代组织越来越多地被视为具有基本自然非线性结构的开放复杂自适应系统,受到可能导致混乱的内部和外部力量的影响。例如,团队建设和团队发展越来越多地被研究为一个天生不可预测的系统,因为不同个人第一次会面的不确定性使团队的轨迹变得不可知。
有人说,基于数学模型和人类行为的心理方面的言语理论中使用的混沌隐喻为描述小型工作群体的复杂性提供了有益的见解,这些见解超越了隐喻本身。
红色的车和蓝色的车轮流移动;红色的只向上移动,蓝色的向右移动。每次,如果前面没有车,所有颜色相同的车都会试图移动一步。在这里,该模型以某种几何模式自我组织,在那里有一些交通堵塞,在一些区域汽车可以以最高速度行驶。
交通预测可能受益于混沌理论的应用。更好地预测拥堵何时发生,可以在拥堵发生之前采取措施驱散拥堵。将混沌理论原理与其他一些方法相结合,产生了一个更准确的短期预测模型(见右侧BML交通模型图)。
混沌理论已被应用于环境水循环数据(也包括水文数据),如降雨量和流量。这些研究产生了有争议的结果,因为检测混沌特征的方法往往相对主观。早期的研究往往“成功”地发现了混沌,而随后的研究和荟萃分析对这些研究提出了质疑,并解释了为什么这些数据集不太可能具有低维混沌动力学。
在艺术(主要是艺术理论)中,一个可能的后后现代时代已经被勾勒出来,强调多重叙事和每个虚构角度都是可能的概念。在某种程度上,这是双社会(三社会)话语的原因,可以在强调主观主义主体的制度交换的情况下加以解释。










![{\displaystyle \psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f[\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbad9689ef6e3759ba8c806bbf568a7d3ff90518)
![{\displaystyle K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{\frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/634f66d2d768bec45cbd9d5b17fea78dd2d2ef88)





